Tabung: Pengertian, Unsur, Sifat, Jaring, Rumus, Dan Contoh Soal
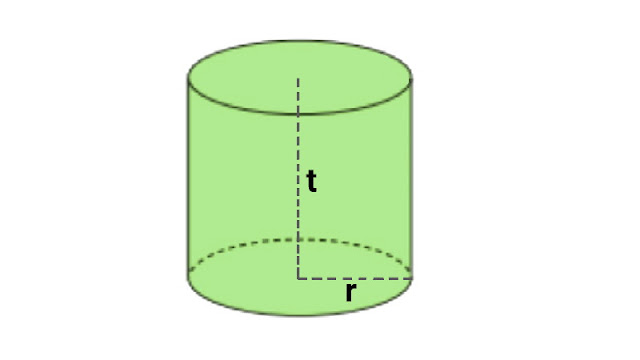 |
| Tabung |
Tabung: Pengertian, Unsur, Sifat, Jaring, Rumus, Dan Contoh Soal - Dalam pelajaran matematika, terdapat materi tentang bangun ruang. Salah satu jenis bangun ruang adalah tabung. Pada artikel ini akan dibahas secara lengkap mengenai pengertian, unsur, sifat, jaring, rumus dan contoh soal tabung.
Tabung merupakan bangun ruang yang tidak memiliki titik sudut, tetapi memiliki dua buah rusuk. Rusuk tabung merupakan keliling lingkaran sisi alas dan sisi atas tabung. Tabung juga disebut sebagai prisma lingkaran. Karena sisi alas dan sisi atas tabung adalah lingkaran kongruen.
Dalam kehidupan sehari-hari, terdapat beberapa benda yang memiliki bentuk tabung. Seperti kaleng susu, kaleng minuman, drum dan lain sebagainya. Selanjutnya kita akan mengenal unsur-unsur tabung.
1. Sisi Tabung
Sisi tabung adalah bidang yang membatasi ruangan di dalam tabung dengan ruangan sekitarnya. Sisi tabung terdiri dari dua buah lingkaran dan sebuah sisi lengkungan berbentuk persegi panjang yang menghubungkan sisi alas dengan sisi atas tabung.
2. Rusuk Tabung
Rusuk tabung adalah perpotongan antara sisi-sisi tabung. Tabung memiliki dua buah rusuk. Rusuk tabung berbentuk lingkaran yang terletak pada sisi alas dan sisi atas tabung.
3. Jari-Jari Tabung
Jari-jari adalah jarak antara titik pusat dengan lengkungan lingkaran. Jari-jari tabung merupakan jarak antara titik pusat lingkaran tabung dengan lengkungan rusuk tabung.
4. Diameter Tabung
Diameter adalah jarak antar lengkungan rusuk tabung yang melewati titik pusat tabung. Diameter tabung merupakan dua kali panjang jari-jari tabung.
5. Tinggi Tabung
Tinggi tabung adalah jarak antara titik pusat lingkaran sisi alas tabung dengan titik pusat lingkaran sisi atas tabung. Tinggi tabung merupakan lebar sisi selimut tabung.
Jaring-jaring tabung terdiri dari dua buah lingkaran yang sama besar dan satu buah persegi panjang. Berikut merupakan contoh gambar jaring-jaring tabung.
Pada gambar jaring-jaring tabung di atas, terdapat dua buah lingkaran yang merupakan sisi alas dan sisi atas tabung. Sedangkan bentuk persegi panjang merupakan sisi lengkung tabung.
Volume tabung adalah seberapa besar ruangan di dalam tabung yang mampu ditempati. Volume bangun ruang dapat dihitung dengan mengkalikan luas alas dengan tingginya.
Alas tabung adalah lingkaran. Sedangkan tinggi tabung merupakan jarak dari sisi alas dan sisi atas tabung. Sehingga, rumus untuk menghitung volume tabung adalah:
V = π x r² x t
Keterangan:
V = volume tabung
π = 22/7 atau 3,14
r = jari-jari tabung
t = tinggi tabung
satuan volume adalah satuan panjang kubik, contoh: m³, cm³, mm³.
L = 2 x π x r x (r + t)
Keternagan:
L = luas permukaan tabung
π = 22/7 atau 3,14
r = jari-jari tabung
t = tinggi tabung
satuan luas adalah satuan panjang persegi, contoh: m², cm², mm².
Penyelesaian:
V = π x r² x t
V = 22/7 x 7² x 10
V = 22/7 x 49 x 10
V = 154 x 10
V = 1.540 cm³
Jadi, volume tabung adalah 1.540 cm³.
2. Diketahui sebuah tabung mempunyai jari-jari 14 cm dan tinggi 10 cm. Berapa luas permukaan tabung tersebut?
Penyelesaian:
L = 2 x π x r x (r + t)
L = 2 x 22/7 x 14 x (14 + 10)
L = 2 x 22/7 x 14 x 24
L = 2 x 44 x 24 L = 2.112 cm²
Jadi, luas permukaan tabung adalah 2.112 cm².
3. Diketahui sebuah tabung memiliki volume 2.310 cm³. Jika jari-jari tabung 7 cm, berapa tinggi tabung tersebut?
Penyelesaian:
V = π x r² x t
t = V : (π x r²)
t = 2.310 : (22/7 x 7²)
t = 2.310 : (22/7 x 49)
t = 2.310 : 154
t = 15 cm
Jadi, tinggi tabung adalah 15 cm.
4. Diketahui sebuah tabung memiliki luas permukaan 1.760 cm². Jika jari-jari tabung 14 cm, berapa tinggi tabung tersebut?
Penyelesaian:
L = 2 x π x r x (r + t)
t = L : (2 x π x r) - r
t = 1.760 : (2 x 22/7 x 14) - 14
t = 1.760 : 88 - 14
t = 20 - 14
t = 6 cm
Jadi, tinggi tabung tersebut adalah 6 cm.
Demikianlah pembahasan mengenai tabung: pengertian, unsur, sifat, jaring, rumus, dan contoh soal. Semoga bermanfaat.
Pengertian Tabung
Tabung adalah sebuah bangun ruang yang dibatasi oleh sisi alas dan sisi atas berbentuk lingkaran, serta sisi lengkung yang disebut dengan selimut tabung. Sisi selimut tabung merupakan lengkungan persegi panjang.Tabung merupakan bangun ruang yang tidak memiliki titik sudut, tetapi memiliki dua buah rusuk. Rusuk tabung merupakan keliling lingkaran sisi alas dan sisi atas tabung. Tabung juga disebut sebagai prisma lingkaran. Karena sisi alas dan sisi atas tabung adalah lingkaran kongruen.
Dalam kehidupan sehari-hari, terdapat beberapa benda yang memiliki bentuk tabung. Seperti kaleng susu, kaleng minuman, drum dan lain sebagainya. Selanjutnya kita akan mengenal unsur-unsur tabung.
Unsur-Unsur Tabung
Setiap bangun ruang memiliki unsur-unsur pembentuk ruangannya. Berikut adalah unsur-unsur tabung dan penjelasannya.1. Sisi Tabung
Sisi tabung adalah bidang yang membatasi ruangan di dalam tabung dengan ruangan sekitarnya. Sisi tabung terdiri dari dua buah lingkaran dan sebuah sisi lengkungan berbentuk persegi panjang yang menghubungkan sisi alas dengan sisi atas tabung.
2. Rusuk Tabung
Rusuk tabung adalah perpotongan antara sisi-sisi tabung. Tabung memiliki dua buah rusuk. Rusuk tabung berbentuk lingkaran yang terletak pada sisi alas dan sisi atas tabung.
3. Jari-Jari Tabung
Jari-jari adalah jarak antara titik pusat dengan lengkungan lingkaran. Jari-jari tabung merupakan jarak antara titik pusat lingkaran tabung dengan lengkungan rusuk tabung.
4. Diameter Tabung
Diameter adalah jarak antar lengkungan rusuk tabung yang melewati titik pusat tabung. Diameter tabung merupakan dua kali panjang jari-jari tabung.
5. Tinggi Tabung
Tinggi tabung adalah jarak antara titik pusat lingkaran sisi alas tabung dengan titik pusat lingkaran sisi atas tabung. Tinggi tabung merupakan lebar sisi selimut tabung.
Sifat-Sifat Tabung
Dari penjelasan unsur-unsur tabung di atas, maka dapat diperoleh kesimpulan bahwa sifat-sifat tabung adalah sebagai berikut:- Tabung memiliki 3 sisi, yaitu sisi alas, sisi atap dan sisi selimut
- Sisi alas dan sis atas tabung berbentuk lingkaran kongruen
- Sisi selimut tabung merupakan bangun persegi panjang
- Tabung memiliki 2 buah rusuk
- Tabung tidak memiliki titik sudut
Jaring-Jaring Tabung
Jaring-jaring adalah gabungan dari beberapa bangun datar pembentuk bangun ruang. Setiap bangun ruang memiliki pola jaring-jaring yang berbeda.Jaring-jaring tabung terdiri dari dua buah lingkaran yang sama besar dan satu buah persegi panjang. Berikut merupakan contoh gambar jaring-jaring tabung.
 |
| Jaring-Jaring Tabung |
Pada gambar jaring-jaring tabung di atas, terdapat dua buah lingkaran yang merupakan sisi alas dan sisi atas tabung. Sedangkan bentuk persegi panjang merupakan sisi lengkung tabung.
Rumus Tabung
A. Volume TabungVolume tabung adalah seberapa besar ruangan di dalam tabung yang mampu ditempati. Volume bangun ruang dapat dihitung dengan mengkalikan luas alas dengan tingginya.
Alas tabung adalah lingkaran. Sedangkan tinggi tabung merupakan jarak dari sisi alas dan sisi atas tabung. Sehingga, rumus untuk menghitung volume tabung adalah:
V = π x r² x t
Keterangan:
V = volume tabung
π = 22/7 atau 3,14
r = jari-jari tabung
t = tinggi tabung
satuan volume adalah satuan panjang kubik, contoh: m³, cm³, mm³.
B. Luas Permukaan Tabung
Luas permukaan tabung adalah luas seluruh sisi-sisi tabung. Perhatikan gambar pola jaring-jaring tabung di atas, tabung terdiri dari dua buah lingkaran dan satu buah persegi panjang. Nah, jumlah dari luas lingakran dan luas persegi panjang itulah yang dinamakan luas permukaan tabung.
Untuk menghitung luas permukaan tabung, maka kita harus mengetahui rumus luas lingkaran. Rumus luas lingkaran adalah π x r². Sedangkan selimut lingkaran dapat dihitung dengan mengkalikan keliling lingkaran dengan tinggi tabung. Dengan begitu, maka rumus untuk menghitung luas permukaan tabung adalah:L = 2 x π x r x (r + t)
Keternagan:
L = luas permukaan tabung
π = 22/7 atau 3,14
r = jari-jari tabung
t = tinggi tabung
satuan luas adalah satuan panjang persegi, contoh: m², cm², mm².
Contoh Soal
1. Diketahui sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Berapa volume tabung tersebut?Penyelesaian:
V = π x r² x t
V = 22/7 x 7² x 10
V = 22/7 x 49 x 10
V = 154 x 10
V = 1.540 cm³
Jadi, volume tabung adalah 1.540 cm³.
2. Diketahui sebuah tabung mempunyai jari-jari 14 cm dan tinggi 10 cm. Berapa luas permukaan tabung tersebut?
Penyelesaian:
L = 2 x π x r x (r + t)
L = 2 x 22/7 x 14 x (14 + 10)
L = 2 x 22/7 x 14 x 24
L = 2 x 44 x 24 L = 2.112 cm²
Jadi, luas permukaan tabung adalah 2.112 cm².
3. Diketahui sebuah tabung memiliki volume 2.310 cm³. Jika jari-jari tabung 7 cm, berapa tinggi tabung tersebut?
Penyelesaian:
V = π x r² x t
t = V : (π x r²)
t = 2.310 : (22/7 x 7²)
t = 2.310 : (22/7 x 49)
t = 2.310 : 154
t = 15 cm
Jadi, tinggi tabung adalah 15 cm.
4. Diketahui sebuah tabung memiliki luas permukaan 1.760 cm². Jika jari-jari tabung 14 cm, berapa tinggi tabung tersebut?
Penyelesaian:
L = 2 x π x r x (r + t)
t = L : (2 x π x r) - r
t = 1.760 : (2 x 22/7 x 14) - 14
t = 1.760 : 88 - 14
t = 20 - 14
t = 6 cm
Jadi, tinggi tabung tersebut adalah 6 cm.
Demikianlah pembahasan mengenai tabung: pengertian, unsur, sifat, jaring, rumus, dan contoh soal. Semoga bermanfaat.